A veces llegas a posts que te gustaría haberlos escrito tú. Stat 101 de Michael Zuschlag es uno de ellos. Trata sobre estadística inferencial aplicada a las pruebas de usuario. Un tema que podría ser bastante árido (que lo es), lo explica de forma amena y fácil de entender. Espero que os parezca tan interesante y útil como me fue a mí.

¿Te gustan los ordenadores, pero odias las matemáticas? ¿Te gusta trabajar en la creación de tecnología punta, pero crees que no tienes la aptitud cuantitativa para ser un programador o ingeniero informático? Entonces, ¡conviértete en un profesional de la experiencia de usuario! Si puedes contar hasta 5 (el número de usuarios en un test de usabilidad), entonces ¡ya sabes todas las matemáticas que necesitas! ¡Todo lo demás es arte! Apuesto a que eres bueno en el arte, ¿no?

¡Ja! ¡Iluso! Resulta que es necesario saber algo de matemáticas para trabajar en Experiencia de usuario. Estar en UX significa que tarde o temprano vas a tener que lidiar con los datos sobre el rendimiento o la satisfacción del usuario, habitualmente de un test de usabilidad. Incluso si te limitas a dejar el diseño y la investigación de usuarios en otras personas, vas a tener que revisar los resultados de la investigación del usuario para mejorar tu trabajo de diseño, por lo que vamos a necesitar conocer algunos de esos conceptos para poder hacer la evaluación de esos datos.

En concreto, necesitas saber un par de cosas sobre estadística inferencial, la rama de la estadística que nos ayuda a determinar lo que razonablemente se puede concluir acerca de la población de usuarios en función de lo que estás viendo en la muestra de usuarios. La estadística inferencial tiene dos objetivos básicos, los dos sobre los datos del usuario:

• Valor de la inferencia. Dado un porcentaje observado o el rendimiento promedio en la muestra de los usuarios, inferir lo que probablemente estaría sucediendo en toda la población de usuarios. Puedes intuir que el promedio o el porcentaje del rendimiento de los usuarios que vemos en una pequeña muestra fácilmente podría no corresponderse con el promedio o porcentaje los usuarios en toda la población. Por ejemplo, podría ocurrir que se obtuviera al azar algunos usuarios que se desempeñaron mejor o peor que los usuarios promedio. El valor de la inferencia explica cuál es la probabilidad de que esto ocurra.
• Relación de la inferencia. Habida cuenta de una aparente conexión entre dos variables en la muestra de los usuarios, inferir si existe algún tipo de relación sistemática o causal entre los dos. Es posible que aparezca un cierto patrón en la muestra. Por ejemplo, puede observarse que los usuarios que comienzan en una determinada página tienen más probabilidades de realizar una compra que quienes comienzan en otra página. Podría ser una coincidencia o pura casualidad. O podría haber algún tipo de relación subyacente. La relación con la inferencia nos dice la probabilidad de que existan una relación sistemática entre dichas variantes.

¿Por qué evitar la Estadística inferencial?

«No me fío de los números»

Si estás calculando un valor de la inferencia o la relación de la inferencia, la estadística inferencial es fundamental para establecer la confianza que debes tener en tus datos. Puedes pensar que no vale la pena molestarse con la estadística cuando el rendimiento general de la prueba es sólo una de las muchas cosas que tienen un peso en el diseño. Pero sin establecer un nivel de confianza para ese rendimiento, ¿cómo puedes saber cuánto pesan en las discusiones sobre tu diseño? ¿Cómo sabes si estás realmente aprendiendo algo de un test de usabilidad o simplemente te estás engañando a ti mismo? Sin establecer un nivel de confianza, ¿cómo puedes convencer a tu cliente sobre la importancia del problema que estás tratando de resolver? ¿Qué haces si un jefazo, por ejemplo Wayne de Finanzas, dice: «Bah, sólo es una prueba con cinco usuarios. Eso no es estadísticamente significativo.» ¿Te encoges de hombros?

¡Oh, el “Sr. Significación Estadística”! Temido por algunos. Tratado con desprecio por los demás. Es como si casi todo el mundo deseara que se fuera. Creo que la mayoría de profesionales de UX contamos con que haya algún “Sr. Significación Estadística” que pregunte si los tamaños de muestra en nuestra investigación del usuario son lo suficientemente grandes. Esto nos da a los UXers la incómoda sensación de que si lo permitimos, el “Sr. Significación Estadística” empezará a decir lo falsos que son los datos de los test de usabilidad con muestras pequeñas. Al igual que Galileo mostrando que la Tierra gira alrededor del sol, puede probar que la credibilidad en las pruebas de usabilidad es nula. Y no podemos permitir que haga eso. Sin embargo, como el solitario incomprendido en una película de clase B, el “Sr. Significación Estadística” en realidad tiene algo valioso que ofrecer a la comunidad de UXers si nos tomáramos el tiempo suficiente para aplacar su ignorancia matemática.

En su lugar, oigo que no merece la pena el esfuerzo de aplicar un análisis estadístico a un test de usabilidad típico con muestras pequeñas, o, es más, que las estadísticas no se aplican a muestras pequeñas, como si ser simple nos excluyera de las leyes de probabilidad. Me han dicho cosas como: «El tamaño de la muestra es demasiado pequeña para el análisis estadístico», que es algo así como decir: «Nuestro barco es demasiado pequeño como para preocuparse de la sobrecarga.»

Algunos creen que es mejor disparar por si acaso al mensajero antes de que digamos cosas inconvenientes. Frases como, «sé que no va a ser importante, con sólo cinco personas, así que ¿por qué molestarse?» Y se van intentando ocultar el problema. Vale. “Sé que mi paracaídas no se despliega correctamente, entonces ¿por qué comprobarlo?” Disculpe, pero es tengo que hacer paracaidismo.

«Estoy siendo cualitativo»

Es legítimo sostener que las estadísticas no son pertinentes en las pruebas de usabilidad con muestras pequeñas, ya que tu interés está en los datos cualitativos y su análisis, en lugar de datos cuantitativos y su análisis. El análisis cualitativo es un acercamiento eficaz y científico perfecto para responder a los tipos de preguntas que desea responder a un test de usabilidad, especialmente cuando se usa como parte del diseño interactivo (es decir, formativo en lugar de prueba sumativa). En ese caso, estás menos interesado en el valor de la inferencia que en las inferencias de las relaciones. No te importa nada cuántos usuarios tienen problemas con tu producto. Como UXer, asumes que habrá problemas con tu producto, y muy a menudo, así será, a pesar de tus mejores esfuerzos como UXer.

Lo que quieres saber es cuáles son esos problemas y, sobre todo por qué ocurren. Sin la habilidad de inferir una relación entre el problema (por ejemplo, el usuario se pierde) y la causa (la etiqueta del vínculo es confusa), no sabrás cómo mejorar el producto. Para inferir relaciones de forma cuantitativa, tienes que anticipar el problema y la causa, y medir o controlar cada uno, haciendo algo más cercano a las pruebas A/B que las pruebas clásicas de usabilidad con muestras pequeñas. A causa de esto, lo cualitativo es mejor que lo cuantitativo cuando estás haciendo pruebas de usabilidad de tipo investigación exploratoria «vamos a poner un usuario frente a esta cosa y a ver qué pasa» y este tipo de pruebas de usabilidad.

Así que definitivamente debes recopilar y evaluar datos cualitativos. Sin embargo, debe hacerse esto porque es la mejor metodología, no como táctica para ignorar las cuestiones estadísticas. A propósito:

• Sólo por llamarlo «cualitativas» no la convierte en cualitativo. Algunos UXers parecen pensar que cualitativa significa simplemente tener un carácter vago en sus informes, que mientras no representas nada con números arábigos, puedes omitir las partes estadísticas. Las frases que usan son «algunos usuarios» y «la mayoría de los usuarios», o muestran los datos en gráficas, en lugar de dar un número preciso o un porcentaje. Cada vez que tratas con cantidades relativas o niveles de algo, tratas con cantidades, y las estadísticas son necesarias. Cada vez que asciende el gráfico, está utilizando las estadísticas, pero no necesariamente las estadísticas inferenciales. Los verdaderos datos cualitativos son historias, secuencias de acontecimientos relacionados y las percepciones, cosas que no se pueden reducir a cantidades sin perder información clave que necesita para hacer relaciones inferenciales cualitativas. La cuantificación de los datos implica necesariamente abstraerlos. No es posible cambiar los datos cuantitativos en datos útiles cualitativos -no tendrás la información narrativa rica que necesitas para el análisis cualitativo.
• Ser cualitativo no es generalmente más barato o más fácil de lo cuantitativo. Mientras que la investigación cualitativa se realiza normalmente en tamaños de muestra pequeños, el tiempo y el esfuerzo dedicado a cada usuario es mucho más alto que la investigación cuantitativa. En la investigación cuantitativa, la recopilación de datos para un usuario puede limitarse a la comprobación de un cuadro para registrar si un usuario completa una tarea o no. En el análisis, ese dato se procesa en un unos pocos ciclos de CPU para obtener los resultados. En la investigación cualitativa, para obtener la información rica que se necesita, necesitas registrar mucho más sobre el desempeño del usuario, dónde se detienen, lo que casi se hace clic, lo que dijo pensando en voz alta, y cómo responde a tus preguntas abiertas. En el análisis, tienes que juntar todo en una narración coherente, que tiene una gran cantidad de ciclos de cerebro. La investigación cualitativa no suele tener tamaños de muestra pequeños con el fin de ser más barato que la investigación cuantitativa, sino porque es muy duro pagar una gran muestra del estudio cualitativo. Mientras que en algunas situaciones la investigación cualitativa es más rentable que cuantitativa, y viceversa, en promedio es lo mismo. Ser cualitativo por defecto no te va a ahorrar tiempo o dinero.
• A veces anticipa los problemas y causas. Si bien la investigación formativa y el diseño iterativo siempre puede descubrir resultados fortuitos, es mejor centrarse en cuestiones concretas de diseño. Aunque esto no excluye usar investigación cualitativa para resolver esta cuestión, al menos implica que puedes conducir un estudio cualitativo: has planteado una hipótesis sobre cómo un diseño concreto afectará al rendimiento del usuario. Se pueden variar los detalles del diseño y medir resultados específicos. Cuando tienes esa especificidad, un enfoque cuantitativo normalmente te dará una respuesta más clara que un enfoque cualitativo.
• A veces es necesario hacer inferencias de valor. La investigación cualitativa puede hablar de la relación entre dos cosas, pero no es adecuado para medir la frecuencia o cantidad de las cosas. Sin embargo, a veces esto es lo que necesitamos saber. A veces no es suficiente para saber si un producto tiene un problema. También tenemos que saber cómo de grave es el problema, por ejemplo, a cuántos de sus usuarios les afecta. Con los recursos de usabilidad limitados, ¿vale la pena el gasto para reparar el problema? ¿Es mejor priorizar otros problemas? ¿O tienes resultados contradictorios de dos fuentes diferentes y necesitas saber cuál de las dos fuentes es mejor? Los valores de inferencias son casi siempre mejores si se hacen con estadística inferencial. Este artículo se centra en hacer valores de inferencias de los resultados con muestras pequeñas en pruebas de usabilidad.
• Los métodos cuantitativos y cualitativos no son mutuamente excluyentes. Puede usar los dos, a veces con la misma muestra de los usuarios para aprovechar las fortalezas de ambos. Por ejemplo, se puede incluir preguntas abiertas en un estudio cuantitativo. Y puedes realizar análisis estadístico inferencial sobre las principales variables cuantitativas en un test de usabilidad con muestras pequeñas, aunque sea una investigación cualitativa.

La importancia de “Ser significativo”

Supongamos que te he convencido que es importante aplicar la estadística inferencial a los problemas de la experiencia del usuario. Entonces, ¿qué es la significación estadística y por qué es necesario prestarle atención? La respuesta es que es sólo una convención social y se puede ignorar.

Vale. Voy a dar alguna explicación sobre cómo llegué a esa respuesta.

Técnicamente, «significación estadística» significa que los resultados que estamos viendo en la muestra de los usuarios no pueden ser atribuidos a la aleatoriedad del muestreo. Por ejemplo, digamos que realizar un test de usabilidad con una muestra ínfima de tres usuarios, y dos de cada tres tienen un problema para completar la tarea. Una tasa de 67% de fracaso suena bastante mal, pero ¿podría ser atribuido a un error de muestreo al azar? En otras palabras, a pesar de tus esfuerzos para conseguir usuarios representativos para hacer la prueba, podrías haber traído a un par de bichos raros que no son capaces de manejar una interfaz de usuario que sería perfectamente clara para casi todas las formas de vida en el planeta. Con una muestra de sólo tres, es bastante probable. Incluso hay gente que lo piensa incluso con cinco usuarios. Podemos esperar que Wayne de Finanzas piense que es muy posible, dado que él no aceptaría resultados siquiera de 5 usuarios.

Sin embargo, Wayne probablemente no distingue el “alfa” de un agujero en el suelo. Esto no es algo que se juzgue forma subjetiva. Se puede calcular la probabilidad de dos fracasos de cada tres en una tarea si hacemos una suposición razonable y tenemos más información.

La suposición

La suposición más razonable es que tu muestra es una muestra aleatoria de la población de usuarios de tu producto. Hacer esta suposición permite las leyes de la probabilidad hacer que el cálculo sea posible. Ahora, por supuesto, no has tomado una muestra estrictamente al azar de los usuarios, donde todos los usuarios de la población tienen la misma oportunidad de estar en su muestra. Es probable que los sacaras de una ubicación geográfica específica, y hay límites en su capacidad de persuadir a los usuarios a participar en la prueba de usabilidad. También tienes un límite de tiempo concreto: tu producto será utilizado por los usuarios en los próximos años, pero ¿has tenido en cuenta a esa muestra del futuro? ¡Ajá! ¡Ninguna muestra al azar!

Sin embargo, intentaste tomar una muestra representativa de los usuarios, usuarios que tienen características similares a los usuarios en tu población: conocimiento, habilidades, e incluso las variables demográficas. A efectos de cálculo estadístico, una muestra representativa es tan buena como una muestra aleatoria. Si estás pensando en cómo tu profesor de psicología te taladró la cabeza con la importancia del azar, seguro que estás pensando en la asignación aleatoria de las condiciones experimentales, no en un muestreo aleatorio para su inclusión en el experimento. La asignación al azar es muy diferente e infinitamente más factible que el muestreo aleatorio. Algunos hasta podrían argumentar que una muestra representativa es mejor que una muestra aleatoria, que los resultados que se obtienen son más coherentes con el desempeño de la población que sólo recogiendo los usuarios al azar. Sin embargo, si piensas en ello, tus métodos de selección de usuarios representativos probablemente dependen de criterios bastante crudos. Por ejemplo, puedes elegir los usuarios con un rango determinado de años de experiencia en informática y web, pero eso es una medida bastante indirecta de sus modelos mentales y de su comprensión real de los ordenadores e internet. Por todos los medios, intenta conseguir grupos representativos de usuarios, aunque probablemente el resultado será prácticamente igual de bueno que una verdadera muestra aleatoria. Que es lo suficientemente bueno para nuestros propósitos.

Entre paréntesis, también tienes que asumir el desempeño independiente entre tus usuarios, donde la posibilidad de que un usuario falle no afecta a la posibilidad de otro que falle. Sin embargo, eso no suele ser un problema en las pruebas de usabilidad, siempre y cuando:

• Probamos usuarios por separado y no como un equipo o focus group para que no se influyan entre sí.
• Tenemos un número por usuario y por cada variable. Por ejemplo, no deberíamos hacer que cada usuario intente la tarea dos veces para obtener un tamaño de muestra de seis en lugar de tres. Podemos, sin embargo, combinar el rendimiento en ambas tareas para cada usuario (por ejemplo, grabar 0, 1 o 2 fallos por usuario) con el fin de utilizar todos los datos, pero manteniendo un tamaño de muestra de tres).

La información adicional

Bueno, vamos a comprar el supuesto de una muestra aleatoria, así que vamos a calcular la probabilidad de que dos de cada tres fallen. A lo que inmediatamente debes preguntarte, la probabilidad ¿de qué? Para el cálculo de una probabilidad, se necesita algún tipo de punto de anclaje, una especie de número para conseguir tracción. Por ejemplo, al lanzar una moneda, para calcular la probabilidad de tener tres caras seguidas, tenemos que tener la posibilidad de tener una cara en un tiro.

En el caso de nuestro test de usabilidad, podemos calcular la probabilidad de que dos de cada tres fallos sean culpa del defecto de nuestra muestra. Lo cual, si lo supiéramos, nos evitaría hacer el estúpido análisis cuantitativo desde el principio. Pero espera: ¿es útil usar un estado hipotético de la población-aunque sea por buscar un argumento sobre la posibilidad de fracasar? ¿Y cuál es el argumento en este caso? En lo que estamos realmente interesados en si esta tasa de fracaso “dos de cada tres” significa que habrá una tasa de fracaso inaceptable cuando el producto esté en el mercado. En otras palabras, queremos hacer un valor de la inferencia.

Los estados de tu población hipotética

Para calcular la probabilidad de esa tasa de fracaso “dos de cada tres” necesitamos un número real para el estado de la población hipotética. ¿Es necesario probar el 50% de los usuarios en la población? ¿El 25%? ¿El 10%? ¿El 0%? Podemos trabajar con los stakeholders para decidir lo que constituye una tasa de fallo aceptable para su uso como un estado de la población hipotética. Una forma de verlo es comparar el costo de arreglar el diseño con el costo de no arreglar el diseño. Puede que incluso Wayne te dé algunas cifras para calcularlo. Por ejemplo, supongamos que rediseñar lo que la falla tiene en promedio un total de 10 horas de trabajo, a 100€ la hora, lo que el coste de una solución es de 1000€.

El coste de no arreglar el diseño puede ser más difícil de cuantificar en dinero. En el software de negocios, un fallo de diseño puede hacer que la tarea lleve más tiempo (que cuesta más tiempo del usuario), reducir el ánimo de los trabajadores, aumento de llamadas de dudas técnicas (que requieren más personal), aumento de la probabilidad de un error indeterminado, y así sucesivamente. Para una aplicación web de consumo, un defecto de diseño puedan molestar a los usuarios, disminuyendo el valor de la marca, lo que se traduce en pérdidas de ventas o una reducción del número de usuarios que no puedes vender a los publicitarios.

Digamos que es una aplicación de negocios, y por cada fallo, los usuarios van a perder 15 segundos (un fracaso en la categoría de “leve molestia”). Si los usuarios cobran 30€ por hora, ese fallo tiene un coste de 0,125€ cada vez que ocurre. Así que si hay más de 8.000 fallos en el tiempo de vida del diseño, entonces vale la pena revisar el diseño (8.000 * 0,125€ = 1000€, el costo de reparación). Digamos que tienes 100 usuarios usando tu diseño una vez por día, en promedio con 250 días de trabajo por año, y la vida útil del diseño es de 2 años. Eso da 50.000 encuentros durante la vida de la aplicación de (100 * 1 * 250 * 2). Así, la tasa de fracaso del punto de equilibrio es de 16% por visita (8.000 / 50.000). Si la tasa de fallo de la población es más del 16%, el rediseño te ahorrará dinero a largo plazo. Si la tasa de fallo de la población es menos de 16%, entonces ahorramos dinero al no arreglar el diseño (teniendo en cuenta sólo los costes de tiempo del trabajador).

El coste total de no reparar un defecto depende del número de usuarios y el número de veces que los usuarios se encuentran el diseño durante la vida útil del producto. Haz el mismo tipo de cálculos en una aplicación de comercio electrónico con millones de usuarios y cientos de millones de dólares en ventas, y verás que vale la pena arreglar un fallo de diseño que haría que una fracción de los usuarios se encuentran el error se vayan a un competidor.

En la práctica, no vas a ser capaz de determinar la tasa de población con tanta precisión. Lo que puedes hacer es calcular un rango de tasas de población jugando con los números que tenemos y hacer algunos cálculos prudentes junto con tus stakeholders:

• Estado Hipotético A: ¿Qué tasa de fracaso consideran absolutamente aceptable? Llamémosle nivel “a quién le importa”.
• Estado Hipotético B: ¿Qué tasa de fracaso consideran que requieren una solución?

Obviamente el Estado Hipotético B es mayor que Estado Hipotético A. El verdadero equilibrio de la tasa de fracaso se ubica entre el Estado A y B, llamémosle “zona x”.

La respuesta es …

Así que estamos tratando de calcular la probabilidad de obtener la tasa de fracaso “dos fallos de cada tres intentos” en los Estado Hipotéticos A y B. Digamos que Wayne dice que ambos tienen que ser del 0%, no el 1% o 0,1%, sino del 0%. El fracaso no es una opción. El jefe se preocupa profundamente por todos los fracasos de los usuarios e insiste en que no exista ningún fallo nunca. Cualquier fallo que se solucione vale la pena. ¿Cuál es la probabilidad de que dos de cada tres usuarios de tu muestra fallen teniendo en cuenta que las posibilidades de fallar en la población total es del 0%?

Respuesta: 0. Acabas de ver dos usuarios que han fallado, así que sabemos que no puede ser 0%. Quiero decir, tal vez ha llegado hasta las dos únicas formas de vida entre millones de usuarios que son capaces de fallar, pero esto significa que la tasa de fallo no puede ser del 0%. Eso fue fácil. Esto es algo que los que se preocupan de los tamaños de muestra pequeños parecen olvidar: con independencia del tamaño de la muestra, si alguna vez observas a los usuarios fallando, ciertamente hay algunos usuarios que fallan con su producto. Es sólo una cuestión de cuántos.

Vamos a hacer lo que realmente hay que hacer para calcular. Una tasa de 0%de fracaso es demasiado ambiciosa. En un sitio web para el público en general, se puede tolerar un pequeño fracaso. Probablemente nos sentiremos muy contentos con un 1% o 2% de tasa de fracaso. Probablemente podemos vivir con un 1% a 2% de nuestros usuarios que realicen un mayor esfuerzo, pidan a ayuda, lean documentación, o, en el peor de los casos, se vayan a otro lado. Tal vez incluso del 5% al 10% sería aceptable siempre y cuando estemos hablando de pequeñas molestias y problemas de reembolso. Por el contrario, si estamos consiguiendo una tasa de fracaso del 50%, incluso si son sólo molestias pequeñas, entonces nuestro sitio web está empezando a parecerse a una zona de desastre de usabilidad. Por ejemplo:

• Estado Hipotético A: 10% fracaso. Definitivamente no se soluciona el diseño.
• Estado Hipotético B: 50% fracaso. Definitivamente arreglar el diseño

Eso coloca al punto de equilibrio entre arreglar y no arreglar en el rango 20-40%. Eso podría ser razonable para algunas aplicaciones de intranet con pequeñas poblaciones de usuarios.

Con respecto a la significación estadística, usaremos el Estado hipotético A. Vamos a revisar Estado hipotético B después.

¿Cuál es la probabilidad de que dos de cada tres usuarios fallen, cuando la tasa de fracaso es del 10% de la población?

Respuesta: 0,028.

Aproximadamente un usuario de cada 36. Esa es una posibilidad bastante baja. ¿Qué significa? Realmente es muy poco probable que la tasa de fracaso sea del 10% de la población. No sabemos cuánto es, pero es evidente que sería improbable que fuera menos del 10%. Es mucho más probable que sea superior al 10%. Esto significa que es muy probable si se deja el sitio web tal como está, la tasa de fallo estará por encima del «a quién le importa». La tasa real estará en la “zona x” o superior, tal vez muy por encima del punto “Realmente Merece la Pena Rediseñarlo” del 50%. Con dos de cada tres o 67% de los usuarios en su muestra fallan, ¿qué debe hacer? Preocúpate. Muestra a los usuarios un poco de amor. Arregla el diseño. Probablemente lo peor que puedes hacer es buscar un punto de equilibrio.

El valor de p

Para los estadísticos, el número 0,028 que he calculado se simboliza por p, por lo que llaman el «valor de p.» El valor de p representa la probabilidad de observar un determinado resultado (2 fallos de 3) dada una situación hipotética de la población (10% de tasa de fracaso). Lo que acabo de hacer es básicamente de lo que se trata casi toda la estadística inferencial. He calculado un valor de p para un resultado de la muestra dado un estado hipotético bien escogidos de la población (una «hipótesis nula» en la jerga de estadística). Luego miré el valor de p y decidí que era demasiado pequeño como para ser plausible: es poco probable que la tasa de fracaso sea del 10% (o menos). Lo más probable es que se trate de más del 10%. Es probable que tengamos algo de lo que vale la pena preocuparse. Ten en cuenta que mientras que un valor de p es un número infinitamente continuo entre 0 y 1, tenemos que tomar una decisión binaria sobre si merece la pena rediseñar el producto o no.

En casi todos los casos, probablemente estarás de acuerdo en que 0,028 es tan baja que tienes que creer que el índice de fracaso real es más del 10%. Pero ¿y si el valor de p fue de 0,10? ¿0,20? ¿0,50? En alguna parte hay que trazar la línea y establecer un criterio. Puedes pensar en el valor de p como la duda sobre el estado de la población hipotética con respecto a los resultados observados. Un valor de p pequeño significa mucha duda sobre el estado de la población hipotética, y más confianza en que el estado real de la población está más en la dirección de tu resultado de la muestra (en este caso, la tasa de fracaso real es mayor del 10%). Un valor de p alto significa que el resultado de la muestra te dará pocas razones para dudar de la población del estado hipotético. Quizás tienes alguna otra razón para dudar de la población del estado hipotético, pero no es debido a los resultados cuantitativos de sus pruebas de usabilidad.

Otra forma de pensar sobre el criterio de valor de p es tu deseo de estar equivocado. Decidimos volver a diseñar el producto a pesar de que sea poco probable que la tasa de fracaso sea igual o inferior a nuestro nivel «a quién le importa». Poco probable, pero no imposible. De hecho con un valor de p de 0,028, en 28 de cada 1000 pruebas de usabilidad, un nuevo diseño definitivamente no vale la pena. Los estadísticos llaman a estas acciones “Error de tipo I” al hecho de no creer en el Estado hipotético de la población A, cuando en realidad es cierto. La probabilidad de un error de tipo I es igual a tu criterio sobre el valor de p, el punto en el tú dices, «yo no me creo ese estado hipotético. Vamos a actuar como que no es cierto».

Por cierto, la probabilidad de un error de tipo I es simbolizada por la letra griega “alfa”. Ya sabes algo que Wayne el de finanzas no distinguiría de un agujero en el suelo.

Determinando la significación estadística

Vale, hemos conseguido un valor de p de 0,028, por lo que tenemos una duda muy alta de que la tasa de fallo de la población sea de 10% o menos; al contrario, tenemos mucha confianza en que la tasa de fallo sea más del 10%. Pero, ¿es estadísticamente significativa? Ahí es donde las convenciones sociales entran en juego

Como UXer, tú y tus stakeholders pueden usar en principio cualquier criterio de valor de p que deseéis en función de la tolerancia al riesgo en tu situación particular. Los científicos, sin embargo, necesitan estandarizar sus procedimientos estadísticos, lo que incluye la selección de un valor para dividir entre dudoso y plausible. En lo que puede ser considerado como un notable ejemplo de cooperación internacional, decidieron como una comunidad que el criterio de la duda es de 0,05. Es una convención social, pero no arbitraria, teniendo en cuenta los límites prácticos de la investigación teórica y lo que los científicos están tratando de lograr. Para los científicos, las decisiones que tomen sobre la base de este criterio influyen en si tienen nuevos conocimientos científicos o no. Para la estadística inferencial, los científicos seleccionaron un Estado hipotético A de la población que representa esencialmente el status quo conocido. Si los científicos observan algo con un valor de p inferior a 0,05 según ese status quo conocido, entonces la conclusión es que el status quo es incorrecto, y que han descubierto algo nuevo.

0,05 es un criterio muy estricto. Básicamente dice que «realmente no puedes desestimar esta información por un error de muestreo y debes tomarla en serio.» Significa que, con una certeza del 95%, debe haber algo más que un error de muestreo. Francamente, hay pocas cosas fuera de las matemáticas que te aseguren una certeza del 95%. Quiero decir, la gente dice «Estoy 95% seguro de tal y tal» todo el tiempo, pero si te pones a contar realmente con qué frecuencia era realmente cierto lo que decían, te saldrá algo así como el 70%. Y estoy 95% seguro de eso.

El valor de p de 0,05 es el criterio científico convencional para la significación estadística. Si un valor de p es igual o menor a 0,05, entonces el resultado de la muestra es «estadísticamente significativo.» Significa que se concluye que un estado hipotético particular de la población es falso. Por otra parte, si el valor de p está por encima de 0,05, «no es estadísticamente significativo». Significa que no se puede concluir que un hipotético estado particular de la población es falso.

Así que, si tuviéramos que seguir esta convención científica, tendríamos que reconocer (dada una tasa de fallo hipotética de 10%) consiguiendo 2 fallos de cada 3 usuarios tiene un valor de p menor de 0,05.

¡Maldición! Estamos haciendo “estadísticamente significativa” una muestra de sólo 3 usuarios!

Mayores efectos se logran convalores de p más pequeños

Ahora, antes de ir a decirles a todos tus amigos que todo lo que necesitas es una muestra de tres elementos para tener “significación estadística”, pensemos en lo que estábamos calculando. El valor de p es concretamente la probabilidad de obtener 2 fallos de cada 3 usuarios con una tasa hipotética de error de 10%. Si sólo un usuario fallara, estaríamos calculando la probabilidad de obtener 1 fallo de cada 3 usuarios con una tasa de falla hipotética de 10%, que es un número diferente.

De hecho, el valor de p en este caso es 0,271. Con un valor p de 0,271 hay más de un 25% de probabilidades de obtener 1 fallo de cada 3 usuarios con una tasa de fallo hipotética de 10%; improbable, pero razonablemente posible. (Es decir, encontrarse 2 de cada 3 fallos es estadísticamente significativo, pero 1 de cada 3 no lo es.)

Tienes un gran riesgo de cometer un error de tipo I si inviertes en el cambio de un diseño cuando sólo uno de cada tres usuarios fallan. Hay una gran probabilidad de que sea una pérdida de dinero.

Por lo demás, puedes que tengas normas más estrictas de credibilidad que la comunidad científica. Después de todo, el 0,05 está lejos de ser imposible. Bueno, para ti, tal vez te interese saber que la probabilidad de obtener tres fallos en tres usuarios con una tasa de 10% de la población es de 0,001 ó 1 de cada 1000. Posible, pero en realidad muy poco probable. Si quieres estar super-extra-mega seguro de que no estás cometiendo un error tipo I en tu rediseño, tal vez sólo deberías rediseñar si tres de cada tres usuarios fallan en el test de usabilidad. Un valor de p de 0,001 se llama, y con razón, una elevada significación estadística. Sí, Wayne, con una simple muestra de 3 personas.

Aquí tienes todos los valores de p para un tamaño de muestra de tres y un estado de la población hipotética de 10% o menos:

valores de p para un tamaño de muestra de tres y un estado de la población hipotética de 10% o menos

Errores Observados	Porcentaje de la muestra	Valor de p
0 o más	0%	1,000
1 o más	33%	0,271
2 o más	67%	0,028
3 o más	100%	0,001

He incluido los porcentajes de la muestra para mostrar que cuanto más se desvía de la muestra por encima del valor de la población hipotética (10% en este caso), menor es el valor de p.

Cuida tus Ps

Estas son las lecciones que debes aprender:

1. Wayne es un idiota
2. No se puede mirar simplemente el tamaño de una muestra y decidir si un resultado es estadísticamente significativo o no. El cálculo del valor de p depende de la diferencia entre el resultado observado y el estado seleccionado de la población hipotética. Cuanto más grande sea la diferencia, más probable es que sea estadísticamente significativo. Por eso dije que Wayne probablemente estaba lanzando una cortina de humo cuando dijo que los resultados con un tamaño de muestra de cinco no eran estadísticamente significativos. Él no podría saber si eran significativos o no, sin saber el estado hipotético seleccionado de la población y el resultado observado. Un resultado puede ser significativo con una muestra de tres. Del mismo modo, un resultado a veces puede no ser significativo con una muestra de 300.000.
3. La significación estadística no es lo realmente importante. La significación estadística incluye la convención social del punto de 0.05, que puede o no ser adecuado para tu situación. Hablando de mí mismo como científico, el punto de corte de 0,05 no es malo. Ha servido a la comunidad científica, y si no tienes otra cosa para continuar, es un punto bueno para usar en tu propio trabajo. Sin embargo, como diseñador de interfaz de usuario, tu objetivo es producir el mejor diseño posible, que es un meta diferente de un científico que intenta establecer nuevos conocimientos. Eso puede implica un punto de corte diferente a 0,05.

A esto es lo que me refería cuando dije que deberías ignorar la significación estadística. Lo más importante que la significación estadística ofrece a las pruebas de usabilidad no es una etiqueta “significativo-o-no” para discriminar los resultados, sino más bien el proceso de cálculo de la probabilidad de un resultado dado, un estado de la población hipotética. En lugar de decidir si tiene o no significación, debes considerar los valores de p. Ellos representan un concepto puramente matemático que se pueden aplicar a cualquier situación. Cada vez que informes del resultado de una muestra, ya sea grande o pequeño, también debes incluir explícitamente el valor de p. Entonces, tú, los diseñadores del proyecto, los stakeholders, o quien esté viendo el resultado, puede decidir por sí mismo lo que debe hacer. Por ejemplo en ABtests.com , estoy francamente cansado de tener que calcular el valor de p para mí mismo. Realmente debería estar a la derecha a la etiqueta «¡Mayor conversión!».

También debería incluir el estado hipotético de la población, a menos que sea implícita. Esto no es necesario en el caso de una prueba A/B, porque se entiende que el estado de la población hipotética es que A y B tienen el mismo tipo de conversión.

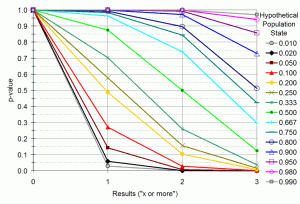
Para ayudarte en el uso de la inferencia estadística en tus propias pruebas de usabilidad, a continuación pongo los valores de p para un tamaño de muestra de tres diferentes estados hipotéticos.

También he preparado tablas para los valores numéricos reales ( http://www.zuschlogin.com/content/blogimages/67/BinomialTable.htm ). Estos valores son los valores de p para obtener un número X de «fracasos» o más, donde un «fracaso» puede ser lo que tú definas, siempre y cuando es algo que tú quieras reducir. Por ejemplo, puede ser cuando un usuario se pierde totalmente en la tarea que le proponemos; o cuando comete un error del que se recupera en una parte específica de la interfaz de usuario; o quizás sólo cuando tarda demasiado tiempo en terminar la tarea. Todo lo que importa es que seamos constantes con todos los usuarios de la muestra. Los gráficos y tablas funcionan para cualquier caso en el que puede dividir los eventos del usuario en dos categorías mutuamente excluyentes y exhaustivas. Para usarlos, debemos:

• Definir qué es un fracaso.
• Seleccionar un Estado hipotético A
• Contar cuántos usuarios fallan.
• Buscar el cálculo para el tamaño de tu muestra y tu Estado hipotético A elegido, y leer el valor de p.
• Si el valor de p es lo suficientemente bajo para ti, considera que la tasa actual es mayor que el hipotético Estado A.

Si tienes «éxitos» (algo de lo que deseas que haya más en tu diseño), entonces conviértelos en fracasos. Convierte también el hipotético Estado A (que es una tasa de éxito) en una tasa de fracaso. Réstala del 100%. Lo siento, no puedo hacer todas las matemáticas por ti.

¿Qué pasa con el Estado hipotético B?

Bueno, ¿cuál es la probabilidad de que los estadísticos determinen un error de «tipo I» cuando no existe tampoco un «error de tipo II»?

Para recapitular, estamos calculando la probabilidad de ver el resultado que vimos en el ejemplo de Estado Hipotético A («¿A quién le importa?»). Este valor de p es la probabilidad de un error de tipo I (cuando el rediseño del producto realmente no vale la pena). Digamos que rediseñas tu producto sólo si dos o más usuarios fallan. Luego en la tabla (o gráfico), vemos que hay una probabilidad de 0,028 de hacer un rediseño cuando definitivamente no debemos. Suena bien. Sigues la tradición científica de mantener la tasa de error tipo I de 0,05 o menos. Pero hay otras consideraciones aparte de mantener bajos el coste del diseño. También podemos preguntarnos, ¿cuál es el coste de no rediseñar una página? ¿Y de no rediseñar cuando definitivamente valdría la pena hacerlo? Esto es un error de tipo II, que es que cuando deberías haber valorado que el estado hipotético fuera erróneo, pero no lo hiciste.

Aquí es donde el Estado hipotético B entra en juego. Representa la tasa hipotética de la población donde definitivamente valdría la pena rediseñar. Digamos que seleccionaste el 50% o más para tu Estado hipotético B. Podemos utilizar las tablas para calcular la probabilidad de que debamos rediseñar del producto cuando definitivamente deberíamos hacerlo. Esa probabilidad se llama «potencia estadística». Réstalo de uno, y tienes tu tasa de error Tipo II, la probabilidad de no rediseñar cuando deberías.

Veamos: 2 de cada 3 fracasos, con una tasa hipotética de 50%, te da 0,500.

Vaya, vaya.

Rediseñando sólo si ocurren dos o más fracasos, estás manteniendo la tasa de error de tipo I en 0,028, pero la tasa de error de tipo II es 1-0,500 = 0,500. Vas a perder la mitad de los defectos de diseño, que son los que más valdría la pena rediseñar. La mitad o más de los problemas que afectan al 50% de los usuarios o más van a llegar a los que usen el producto final. ¡Habrá errores frecuentes en la interacción! ¡Tardarán en completar las tareas! ¡Perderemos ingresos! ¡Habrá motines de usuarios! ¡El colapso de la civilización!

Hambrientos de poder

En las pruebas de usabilidad, un error de tipo II es tan malo como un error de tipo I. Hay que minimizar la probabilidad total de error equilibrando los tipos I y II de probabilidades de error. Así es como fijamos nuestros estados hipotéticos, siendo el Estado A un “definitivamente no merece la pena el rediseño” y el Estado B un “definitivamente merece la pena el rediseño”, y el punto de equilibrio cualquiera en la zona en el medio. Las desviaciones de dicha zona en uno u otro sentido son igualmente malas.

Esto contrasta fuertemente con la investigación científica, donde los errores de Tipo I son peores que los errores de Tipo II. Un error de Tipo I significa que estás descubriendo algo que no es verdad, lo que socavaría la credibilidad de la ciencia y daría pie a un montón de gente a hacer cosas innecesarias (y posiblemente peligrosas) sobre la base de información errónea. Aumenta la probabilidad de que dos hechos contradictorios sean «probados» estadísticamente, lo que causaría una confusión infinita. Un error de tipo II en la ciencia significa que un descubrimiento tendrá que esperar para otro día. Permite a la ciencia ser conservadora, a adoptar una actitud escéptica ante las nuevas ideas hasta que sean empíricamente apoyadas con gran confianza.

Con esto en mente, volvamos a nuestra mesa para una muestra de tres. ¿Qué tipo de resultado sería el mejor balance de los errores de tipo I y II? Echemos un vistazo a un fallo de cada tres. Teniendo en cuenta un Estado hipotético de Población A, de 10%, la tasa de error Tipo I es 0,271. Teniendo en cuenta un Estado hipotético de Población B del 50%, el poder estadístico es 0,875, con una tasa de error tipo II de 0,125. Esos no son grandes probabilidades, pero son un mejor equilibrio que 0,028 y 0,500.

Teniendo en cuenta tus opciones en este ejemplo particular, me parece que deberías solucionar todos los problemas que detectes en cada usuario. Este parece ser el mejor equilibrio de poder estadístico y la tasa de error de tipo I en un tamaño de muestra de tres con el estado hipotético seleccionado. La estadística inferencial para las pruebas de usabilidad se reduce a esta selección de un resultado crítico tan mínimo (1 en este caso) para decidir si rediseñas el producto o no. Al informar sobre tus decisiones, debes informar del resultado crítico y su tasa de error de Tipo I y el poder para que su público entienda la probabilidad de que pudiéramos estar equivocados en nuestras decisiones. ¿Y la significación estadística? A la porra la significación estadística. Si calculas la tasa de error de Tipo I y el poder, entonces no tienes necesidad de declarar la validez o no de la significación estadística. Incluso el tamaño de la muestra es irrelevante.

Justicia estadística

Fíjate que hay un compromiso entre la tasa de error tipo I y el poder estadístico. Rediseñar cuando dos de cada tres usuarios fallan significa una baja tasa de error de tipo I (0,028), pero con poco poder (0,500). Rediseñar cuando uno de cada tres usuarios fallan no significa un buen poder estadístico (0,875), pero tendrías que comprometer las tasas de error tipo I para conseguirlo (0,271). Eso parece justo. No puedes tenerlo todo.

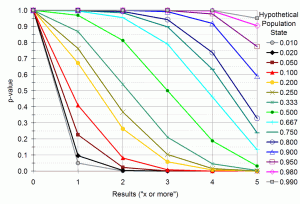
¿Y si no quieres renunciar? Tal vez no puedes elegir entre aceptar un error de tipo I de 0,271 o el poder estadístico de 0,500. Digamos que simplemente no te gustan esas opciones. Significa demasiados errores, rediseñar cosas que no necesitan ser rediseñadas con demasiada frecuencia; o demasiadas cosas que necesitan ser rediseñadas no son rediseñadas. Tal vez los errores de tipo I o II son demasiado costosos para aceptar ese tipo de tasas. Hay algo que puedes hacer al respecto: aumenta el tamaño de la muestra. Echa un vistazo a una muestra de cinco, por ejemplo (ver también la tabla de datos http://www.zuschlogin.com/content/blogimages/67/BinomialTable.htm )

Específicamente, mira la consecución de dos de cada cinco: la tasa de tipo I para el 10% es 0,081. No está mal. No muy lejos de la norma de la significancia estadística para los científicos. El poder estadístico para el 50% es 0,813. Tampoco está mal. Francamente la mayoría de los científicos sería muy feliz con ese tipo de poder. Como dicta tu intuición, las muestras de mayor tamaño reducen la tasa de error. Una muestra mayor significa una confianza mayor en los resultados, y una menor probabilidad de que pienses de forma errónea en un sentido u otro. Sin embargo, no es como que haya un cierto umbral de muestra mágico que asegure que los resultados son fiables. Es todo una cuestión de grado. Una muestra más grande es como un microscopio más grande, que permite detectar de forma más fiable las diferencias más pequeñas en las cosas. Una muestra más grande significa pruebas de usabilidad más caras, por lo que sólo tienen sentido si lo que necesitas es ahorrar en los costes de los errores de tipo I y II. Hay justicia estadística en el mundo. ¿Quieres generar menos errores? Entonces es mejor que estés dispuesto a gastar más. Recoges lo que siembras.

(Para más información sobre cómo seleccionar un tamaño de muestra para una prueba de usabilidad, véase Lewis, JR, (2006) “Sample sizes for usability tests: Mostly math, not magic.” Interactions, 13 (6), p29-33. Fíjate sin embargo que Lewis sólo se refiere a lograr el poder estadístico suficiente, y realmente no analiza las tasas de error de tipo I. Por otra parte, en muchos proyectos, como cuando diseñas para una gran población de usuarios, eso es apropiado porque entonces merece la pena arreglar un detalle de diseño incluso si una fracción muy pequeña de tus usuarios tiene un problema; los errores de tipo I ya no significan un problema real y lo único que necesitas especificar es el estado hipotético B)

Si alguna vez te has estado preguntado por qué los test de usabilidad trabajan muestras de 3 a 5 usuarios, ahora puedes verlo desde un punto de vista estadístico, lo que no está tan mal. De hecho tienes muchas probabilidades de detectar serios detalles de diseño que afectarían a la mayoría de tus usuarios mientras no pierdes el tiempo en detalles que afectan a unos pocos usuarios. Lejos de ser una amenaza a las prácticas de usabilidad, la estadística inferencial las valida. Desde una perspectiva estrictamente racional y matemática de minimización de costes debido a (1) hacer rediseños innecesarios, (2) dejar que los defectos de diseño lleguen a la fase de producción y (3) realizar test de usabilidad, las muestras pequeñas son a menudo la solución óptima.

La limitación principal de una muestra pequeña es que genera una gran incertidumbre acerca de cómo de grande es un problema dado una vez que has decidido que tienes uno. Por ejemplo, podemos saber que es muy probable que afecte al menos al 10% de los usuarios, pero es bastante plausible que el valor real sea entre 10% y 80%. Para la mayoría de las situaciones usabilidad, tal imprecisión es aceptable. Si en cualquier caso vas a arreglar todos los problemas detectados, ¿a quién le importa cuáles son los peores?

Si todavía desconfías de las muestras pequeñas, olvida las matemáticas y míralo de esta manera: si un problema se presenta en una gran parte de tu población de usuarios, es muy probable que lo veas en una muestra pequeña; si el problema se presenta en una porción muy pequeña de tus usuarios, es muy poco probable que lo vea en una muestra pequeña. La muestra pequeña en pruebas de usabilidad, en otras palabras, son una red de malla grande, ideal para la captura de grandes problemas -que son los que al cliente le preocupan en primer lugar.

También hay justicia estadística en los propios errores, en el sentido de que si cometes un error, probablemente no será un error grave. En este ejemplo con poder estadístico de 0,813, tienes una posibilidad de 0,187 de que un defecto de diseño que afecte al 50% o más de tus usuarios. ¿Podría afectar a muchos más que el 50%? Claro que es posible, pero no probable. Mira la tabla para ver la probabilidad de decidir no corregir un defecto que afecte al 80% de los usuarios: 0,007. Lo más probable es que si cometes un error de tipo II, será para un problema cerca de la marca del 50%. Lo mismo sucede con los errores de tipo I. Si al final terminas arreglando un defecto que no merece la pena arreglar, es más probable que ayude al 9% de los usuarios que al 1%, lo que puede no ser rentable, pero no es una total pérdida de recursos de diseño, sobre todo si yo personalmente estoy dentro de ese 9%. El castigo es proporcional al crimen.

Resumen de criterios

Problema: usar estadística inferencial para tomar deciones racionales de rediseño basadas en tests de usabilidad con muestras pequeñas.

Posible solución:

• Con tus stakeholders, elige los estados hipotéticos A y B.
  • • estado hipotético A de la población: un acuerdo sobre la tasa de fracaso de la población para la cual no merece la pena el rediseño.
    • estado hipotético B de la población: un acuerdo sobre la tasa de fracaso de la población para la cual definitivamente merece la pena el rediseño.
• Usando las tablas de este post, busca los valores p de los estados A y B para el tamaño de tu muestra.
• Selecciona un resultado crítico que equilibre estos valores de p, dándote una baja probabilidad para el estado A y una alta probabilidad para el estado B.
  • • El valor de p para el estado hipotético A es tu probabilidad de error de Tipo I – el caso de que rediseñar algo definitivamente no merece la pena.
    • El valor de p para el estado hipotético B es tu poder estadístico – el caso de que rediseñar algo definitivamente merece la pena.
• Si no hay un resultado posible con combinaciones aceptables de p, entonces aumenta el tamaño de la muestra.
• Si observas a los usuarios fallando en o por encima de tu resultado crítico elegido, deberías rediseñar el producto.
• Utiliza el análisis cuantitativo para decidir cómo rediseñar el producto.

Eso es todo. Haz tus elecciones y apuesta por ellas.

El rincón del geek de las estadísticas

Todas las probabilidades en este puesto y en las tablas son cálculos binomiales de una cola. Uso cálculos de una cola porque en un test de usabilidad (a diferencia de la investigación científica de carácter teórico), en general no hay interés en los casos en que la tasa de fallo de la población es menor que el valor de la hipótesis nula, todo lo que importa es si tienes que rediseñar el producto o no. Además, con tamaños de muestra como estos, necesitas todo el poder estadístico que puedas obtener.

Los test de estadística binomiales no hacen suposiciones sobre la normalidad de la distribución de la muestra u otras cosas que hacen los test de parámetros, lo que los hace ideales para los tamaños de muestra pequeños de los test de usabilidad con pequeñas muestras. Su principal desventaja es que está limitada a eventos binarios (por ejemplo, éxito o fracaso). Si estás tratando con promedios o más de 2 categorías de rendimiento, otros test estadísticos son más apropiados, pero más complicados de usar correctamente.